學苑撰文

難以想像，本來只會算0和1的「蠢玩意」，卻能為我們解決生活上各式各樣的問題。這個令電腦能夠執行以0和1序列組成的指令，而變得聰明的神奇魔法，就是今天我想分享的主題 ── 「演算法」了。

演算法是甚麼？

演算法（algorithm）是電腦科學非常重要的一部分。從定義來說，演算法是可以解決某些問題的有效方法之有限集合（finite set）。聽起來好像很複雜，就讓我舉一個例子來說明吧！

以「潔手」為例，只要完成以下（Ａ）或（Ｂ）的各個步驟，就能解決「潔手」問題：    

故此這些步驟可以稱為「潔手的演算法」，因為演算法就是透過一系列動作解決特定的問題。

演算法如何運作？

基本上電腦能解決的問題，都是通過0 和 1的運算來實現。無論是基本的四則運算，即加、減、乘、除，還是複雜的任務例如以人工智能按用戶喜好排序推薦電影等，背後都離不開演算法。為了令大家更容易明白演算法的運作，下文我將透過兩個例子跟大家一探究竟。

1.    插入排序法

將數列分成已整理和未整理的兩部分，在未整理部分中挑選一個數字，按數值大小放在已整理部分中正確的位置。重複這個步驟，直至未整理部分的項數變為0。

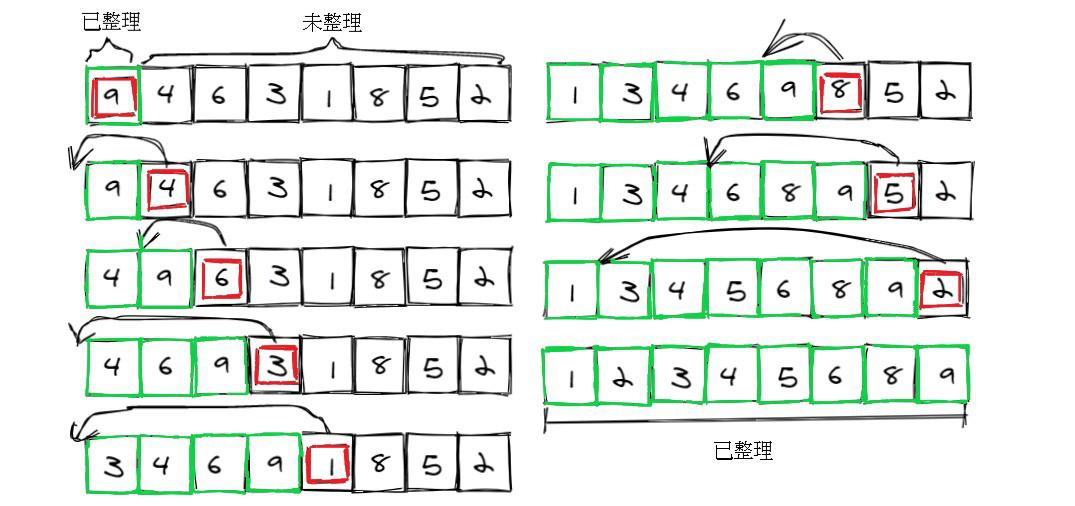
圖1：插入排序法

2.    快速排序法

在數列中隨機抽取一個數字，以此為參考值，將數列分成小於和大於該數的兩個子數列。在子數列中分別重複這個步驟，直至完成排序。

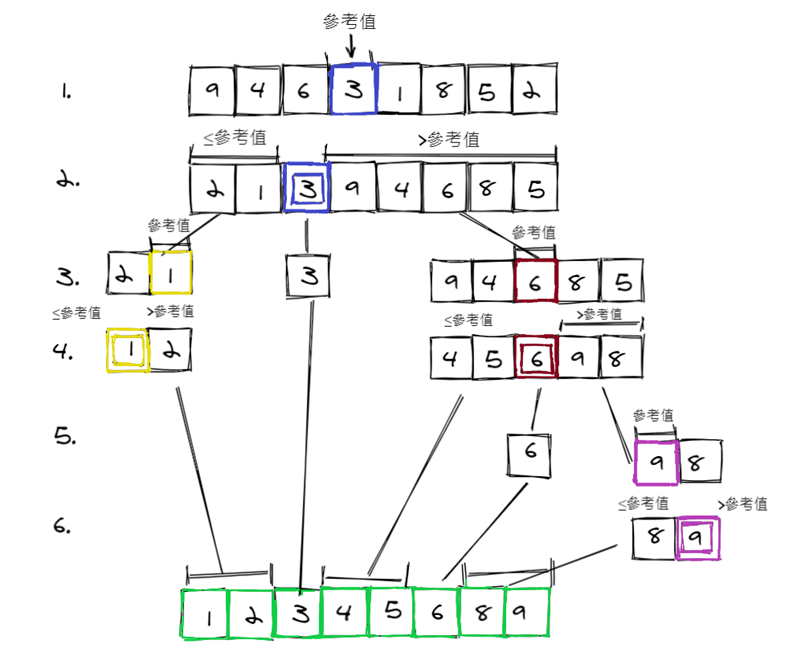
圖2：快速排序法

演算法與「時間複雜度」

以上兩種排序法中，哪一種比較快？這就要看它們的「時間複雜度」了。

「時間複雜度」是描述演算法中輸入項數（n）與運行所需時間之間關係的函數，通常以大O符號表示。

常見的「時間複雜度」例子：

   O（1）：    判斷單雙數（判斷1位數 和100位數所需時間是一樣的）

   O（n）：    加減法（100位數加減所需時間比1位數加減所需時間多100倍）

   O（n²）：   長乘法（100位數乘法所需時間比1位數乘法所需時間多100*100 = 10,000倍）

要留意的是，計算「時間複雜度」時會假設n非常大，因此我們只取增長速度最快的項（通常是最大指數的項），亦會忽略係數，例如：

                                O（3n³ + 2n + 5）→ O（3n³）→ O（n³） 

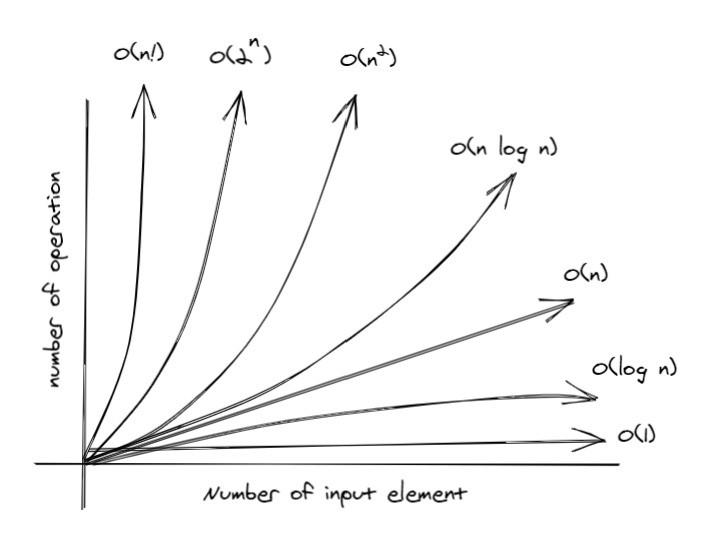
圖3：不同時間複雜度的比較

插入排序法的平均時間複雜度為O（n²） ，而快速排序法的平均時間複雜度則為 O（n log n） 。           

回到上面的問題：兩種排序法中到底哪種比較快？這就交給大家思考了！

作者簡介：

吳沛熹，中四學生，就讀於荃灣官立中學。於小學四年級加入香港資優教育學苑， 積極參與各種課程。對電腦十分感興趣，希望能學到更多有關人工智能的知識，並以此為職業路向。平時亦喜歡做運動調劑身心，最常做的運動是籃球和排球。